As discussed in last month’s article, in Levels 1-9, students learn the basics of Geometry. Students will build upon this foundation in Levels 10-23 to improve their spatial sense through learning Transformations. Transformations is the focus of CTM Geometry Booklets in Level 10-13. Transformation knowledge is further advanced in Booklet 22 for Levels 14-23.
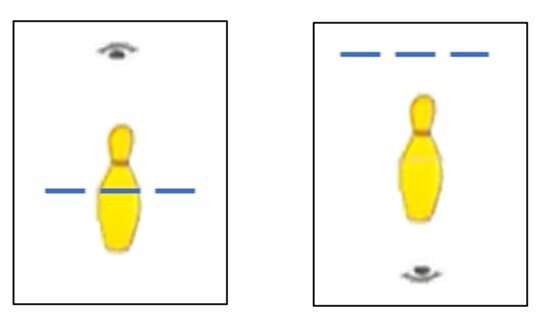
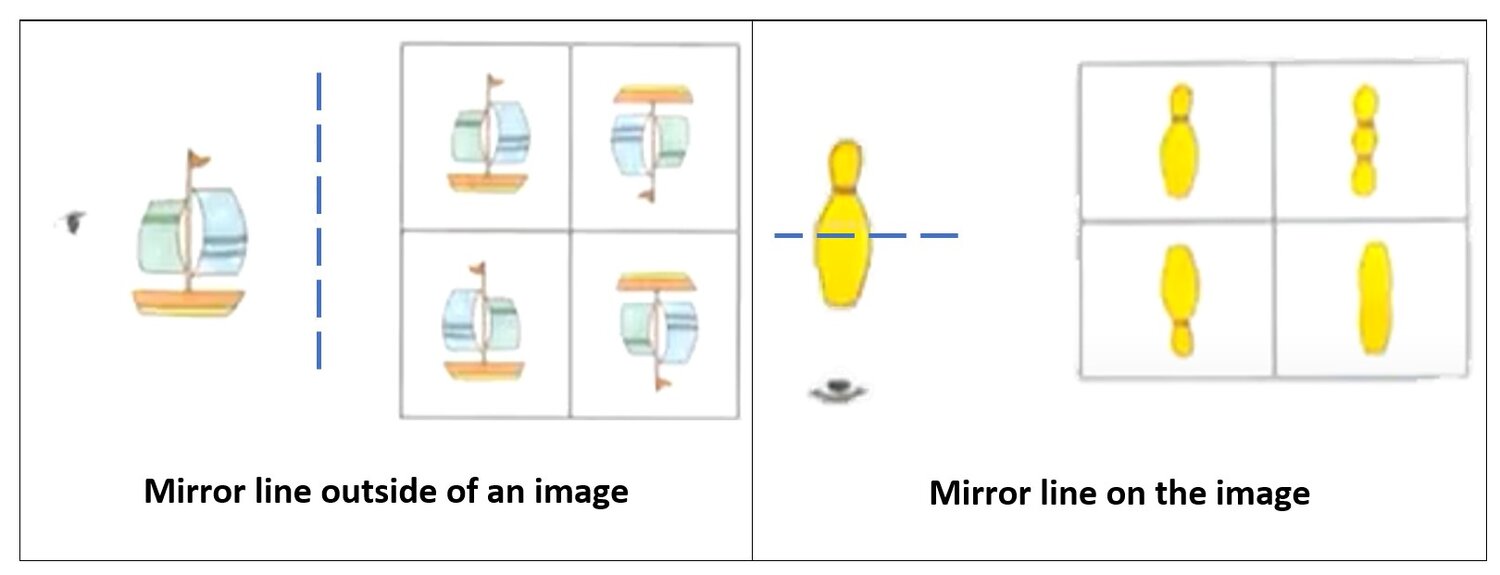
The first Geometry topic, students will learn in Level 10 is mirror images. This is a topic that many students struggle with. Students will learn how objects look differently when reflected off a mirror plane. Use the mirror teaching tool to explain the concept to students. There are two different placements for the mirror. It could be outside the image, or the mirror line could be on the image as shown below. It is also important to point out the eye to the student. The placement of the eye will let the student know which way the reflective part of the mirror will face. Let the students visual how a picture would like if it is reflected in a mirror, and then students should use the mirror to check their answers. To increase students’ proficiency, determine if each of the multiple-choice answers could be made using mirror reflection and determine where the mirror should be placed to make that image. See explanations of the two examples at the end of this article. Although students may struggle with this topic at first, through sufficient practice, the topic will become easier.
Mirror images is a crucial topic because it is the basis of transforming figures. First students will identify the transformations in freehand and then on grids. There are three types of transformations students will learn about- translation, reflection, and rotation. Students will understand rotation, shifting, and parallelism by shifting figures and finding the figure that fold exactly over the other figure. When coaching students to translate, take one vertex at a time and then connect the vertices. Reflection is the basis of learning line symmetry. Rotation is the most difficult among the three. To make rotations easier, student may draw the figure on another piece of paper, or their Key & Note, and then rotate the paper to find the answer. Make sure students know the symbols.

Now that students know these three transformations, students can now identify Congruency, Similarity, and Symmetry. There are three components of Symmetry: finding shapes with symmetry and then identifying shapes that have line or rotational symmetry. A figure that has both halves match exactly when folded along a straight line is called a line-symmetrical figure. That straight line is known as a line of symmetry. A figure rotated 1800 that can overlap with the original is said to point-symmetrical, and the center of the rotation is called the point of symmetry. It is important that congruent figures are the same size and shape regardless of orientation. Similar figures look at both magnifying and reducing. First students simply identify similar images and then they will draw their own similar figures on grid paper. Students will count the length of the line and then will multiply by whole number to enlarge or a fraction to reduce. The number you multiply by is known as the ratio of similarity.
The skills needed to solve these higher-level questions were gradually introduced in the lower levels. By completing these booklets, students will develop their spatial sense, and be more confident as they prepare for more complex topics. Next month, we will look at how students will apply this knowledge to three-dimensional shapes.
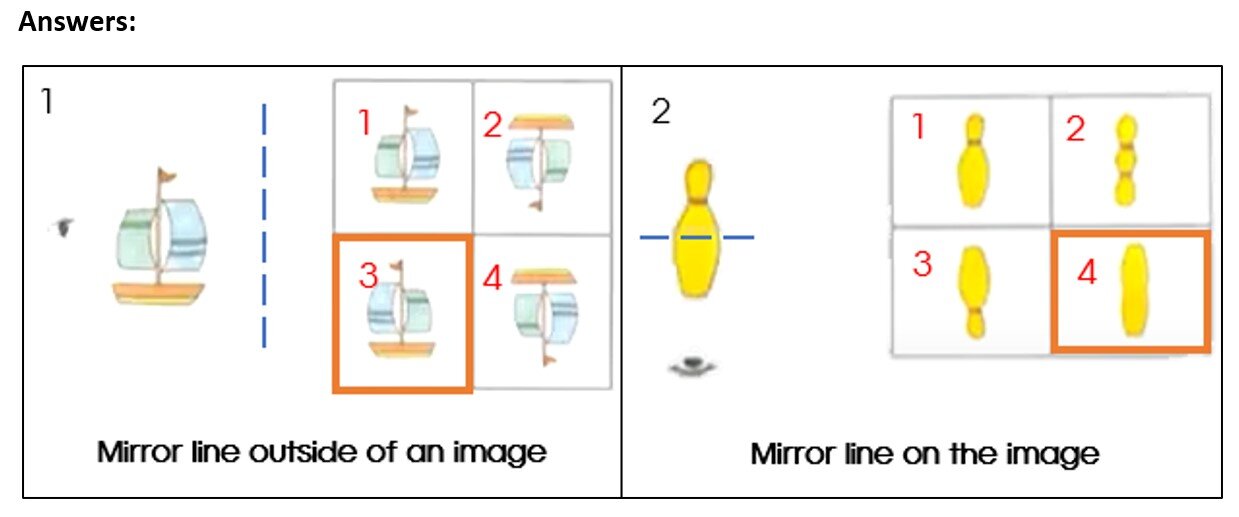
1. Image 1 is a translation; Image 2 is a rotation of 1800; Image 4 is a reflection, but the line and eye would be in placement shown below. All three of these choices can be easily eliminated because due to the placement of the mirror line, the ship would not be upside down; and Image 1 has the same orientation as the original.
2. Image 1 is translation; Image 2 is a reflection if the eye was in a different place as shown on the left; Image 3 is a reflection if the mirror line was outside the image as shown on the right. Images 1 and 3 should be eliminated first because the mirror line in on the shape and therefore it will not look like a traditional bowling pin in the final answer.